Read this article in Hindi to learn about the application of market principle to projects. The applications are:- 1. कुल लाभों का अधिकतमीकरण-निश्चित बजट (Maximisation of Total Benefits-Fixed Budget) 2. कुल लाभों का अधिकतमीकरण-परिवर्तनशील बजट (Maximisation of Total Benefits-Variable Budget).
बाजार नियम की प्रयोज्यता का दो प्रकार से विश्लेषण किया जा सकता है:
(1) कुल लाभों का अधिकतमीकरण-निश्चित बजट (Maximisation of Total Benefits-Fixed Budget),
(2) कुल लाभों का अधिकतमीकरण-परिवर्तनशील बजट (Maximisation of Total Benefits-Variable Budget) ।
ADVERTISEMENTS:
हम बाजार नियम की प्रयोज्यता की उपरोक्त दो श्रेणियों का विस्तार में वर्णन करते हैं:
Application # 1. कुल लाभ का अधिकतमीकरण-निश्चित बजट (Maximisation of Total Benefits-Fixed Budget):
(i) विभाज्य परियोजनाएं (Divisible Projects):
यदि हम कल्पना करते हैं कि परियोजनाएं विभाज्य है; तो कार्य तब सरल होगा जब परियोजना X पर मुद्रा की एक इकाई का व्यय किया जाता है, इसकी अवसर लागत इसे परियोजना Y पर व्यय न करने से खोया हुआ लाभ है तथा विलोमत।
शुद्ध लाभ तब अधिकतम होगा जब कुल लाभ – कुल लागतें उच्चतम हो । यह तब प्राप्त होता है यदि MBx/MBy = MCx/MCy । आइये हम कल्पना करें कि कुल राशि G दो परियोजनाओं X और Y पर व्यय करनी है ।
ADVERTISEMENTS:
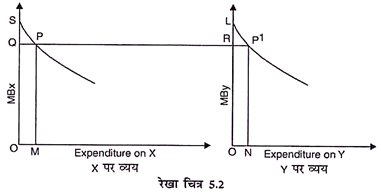
यदि G को उनमें इस प्रकार विभाजित किया जाता है कि OM को X पर व्यय किया जाता है तथा ON को Y पर, कुल लाभ उच्चतम है क्योंकि OM से सीमान्त लाभ PM, ON से सीमान्त PN के बराबर हो जाता है ।
यह इस मान्यता के अधीन ऐसा होगा कि MC एक रुपये के बराबर है तथा इसलिए MBX,MBY के बराबर होनी चाहिये यह रेखाचित्र 5.2 की सहायता से दर्शाया जा सकता है ।
रेखाचित्र 5.2 में OM + ON = G निश्चित बजट । X से कुल लाभ OMPS है तथा Y से ONP1L । X से सीमान्त लाभ PM है तथा Y से P1N तथा वे बराबर है क्योंकि दोनों प्रकरणों MC एक रुपये के बराबर है । PM = P1N, अत: MBx/MBy = MCx/MCy की शर्त पूरी हो जाती है ।
ADVERTISEMENTS:
(ii) पिण्डित परियोजनाएं (Lumpy Projects):
पिण्डित परियोजनाओं के प्रकरण में अर्थात स्पष्ट व्यय श्रेणियों में कोषों का निर्धारण (अर्थात सरकारी विभागों के बीच) सीमान्त अभिगम प्रयोज्य नहीं है । यदि हम प्रत्येक परियोजना से कुल लाभों की तुलना करते हैं और सबसे अधिक लाभप्रद का चयन करते हैं अथवा कुल लाभों की कुल लागतों से तुलना करते है और उनका चयन करते हैं जिनसे शुद्ध लाभ उच्चतम है तो हम ठीक परिणाम प्राप्त नहीं कर सकते क्योंकि विभिन्न परियोजनाओं पर परिव्यय भिन्न होते हैं ।
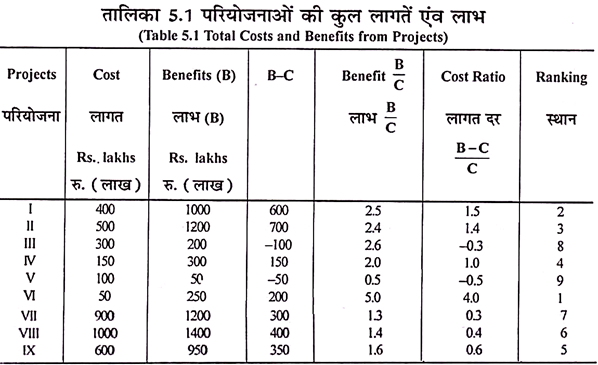
अत: हमें परियोजनाओं को B/C अनुपात के आधार पर स्थान देना होगा । एक वैकल्पिक अभिगम है परियोजनाओं को B-C/C अनुपात के आधार पर स्थान देना एक अनुपात जो लागत पर प्रतिफल का दर देता है । दोनों प्रकरणों में स्थान देने की स्थिति वही होती है ।
तालिका 5.1 में प्रत्येक परियोजना की लागत का माप रुपयों के आवश्यक व्यय द्वारा किया जाता है । लाभ का अर्थ है प्रत्येक परियोजना का कुल लाभ । रेखा चित्र 5.2 के सन्दर्भ में परियोजना Y का कुल लाभ ONP1L क्षेत्र है और इस पर परिव्यय ON है । प्रत्येक परियोजना के लागत और लाभ, ऊपर की तालिका में एक ही प्रकार से दर्शाये गये हैं ।
Application # 2. कुल लाभों का अधिकतमीकरण-परिवर्तनशील बजट (Maximisation of Total Benefits-Variable Budget):
परिवर्तनशील बजटों के प्रकरण में, दो समस्याओं का समाधान अवश्य किया जाना चाहिये । एक कुल बजट के आकार के निर्धारण से सम्बन्धित है तथा दूसरी सार्वजनिक परियोजनाओं के चयन से सम्बन्धित है ।
इस स्थिति में सार्वजनिक परियोजनाओं की अवसर लागत को निजी परियोजनाओं से खोये लाभों के संदर्भ में पुन: परिभाषित करने की आवश्यकता है जो साधनों के सामाजिक प्रयोग की ओर स्थानान्तरण के कारण त्यागे गये हैं ।
यदि सार्वजनिक योजनाएं विभाज्य हैं, तो शुद्ध लाभों के अधिकतमीकरण का कार्य है (∑B-∑C) हुए, जिसमें सार्वजनिक एवं निजी दोनों परियोजनाओं के लाभ और लागतें सम्मिलित है । इसकी प्राप्ति तब होती है जब सार्वजनिक परियोजना पर खर्च किये गये अन्तिम रुपये से प्राप्त सीमान्त लाभ निजी परियोजना के बराबर होता है ।
क्योंकि निजी क्षेत्र में व्यय से सीमान्त लाभ 1 रुपये के बराबर होता है तो सार्वजनिक क्षेत्र में भी ऐसा ही होगा । अब हम पिण्डित परियोजनाओं का प्रकरण लेते हैं । निजी क्षेत्र का B/C अनुपात 1 रुपये के बराबर लिया गया है । सार्वजनिक परियोजना तभी आरम्भ की जायेगी यदि B/C अनुपात 1 से बढ़ता है । इसलिये, यह सुझाव देता है कि तालिका 5.1 में केवल I, II और VI परियोजनाएं आरम्भ की जायेंगी ।
ऊपर, हमारा लक्ष्य यह दर्शाना रहा है कि सरकार की साधन उपयोग करने की गतिविधियों का स्तर तथा विभिन्न गतिविधियों में उनके आबंटन का निर्धारण ‘इष्टतम साधन आबंटन’ के उसी मूलभूत नियम द्वारा किया जाता है जो अर्थव्यवस्था के निजी क्षेत्र में प्रयुक्त होता है ।
यह सीमान्त सामाजिक लागतों और लाभों की समानता है । यह नियम चाहता है कि प्रत्येक सरकारी गतिविधि को उस स्तर तक विस्तृत किया जाये जिस पर गतिविधि से प्राप्त सीमान्त सामाजिक लाभ सामाजिक लागतों के बराबर हो ।
सीमान्त सामाजिक लाभ (MSB) समग्र समाज के सदस्यों की सरकारी व्यय से प्राप्तियां है । सीमान्त सामाजिक लागतों (MSC) को निजी क्षेत्र के उत्पादन से लाभों के रूप में लिया जाता है । जिन्हें साधनों के सार्वजनिक उपयोग की ओर स्थानान्तरण के कारण त्यागा जाता है ।
प्रत्येक सार्वजनिक गतिविधि का इष्टतम स्तर तब प्राप्त होता है जब सभी गतिविधियों से सीमान्त सामाजिक लाभ (MSB) एक दूसरे के बराबर होते हैं । उदाहरणार्थ, शिक्षा पर खर्च किये गये अन्तिम रुपये से समाज को वही लाभ प्राप्त होने चाहिये जो सुरक्षा पर खर्च किये गये अन्तिम रुपये से होते हैं ।